Demo Video

The video goes through a typical usage scenario using Fredo-Editor.

Walkthrough

Launch

Start Fredo Editor with the fredo command in your shell.

Opening an Image

Select the File > Open menu to load an image. Currently .jpg, .bmp, .png formats are supported.

View

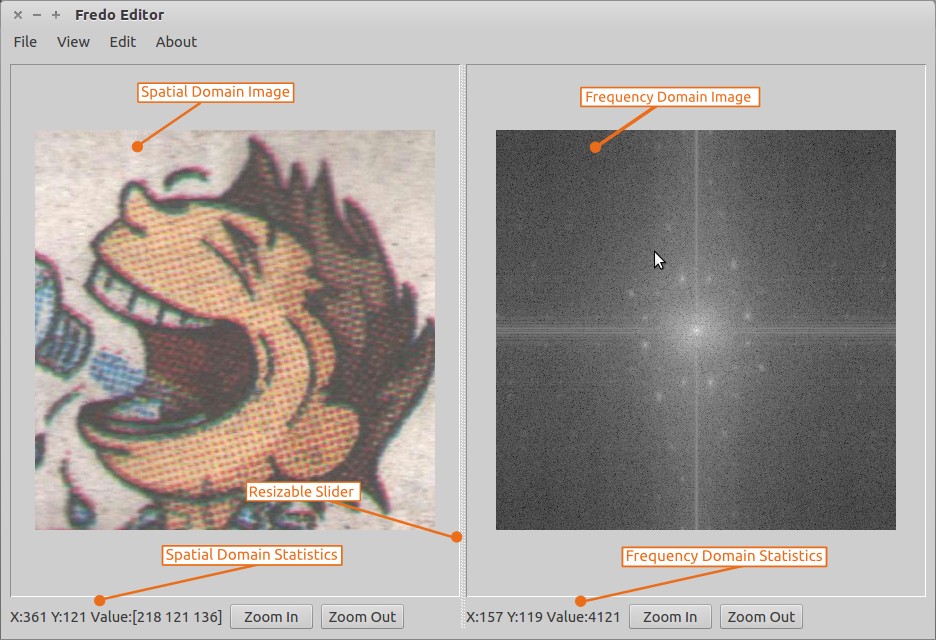
Opening an image displays it and its 2D Discrete Fourier Transform. The transform is shifted such that the highest frequency component is at the centre. To compute the the fourier transform, the image is first internally converted into the YUV color space. In the YUV space, the Y component represents the intensity and is used to compute the Fourier Tranform. Since the result of the Fourier transform is complex, only its magnitude is visualized on the right hand side. Within the magnitude, the peaks are several times grater than the rest of values. To effectively visualize it, we plot the log of the magnitude, instead of the magnitude itself.

Brush

Selecting the Edit > Brush menu opens the configuration options for a brush.

Currently only a Square Brush is supported.

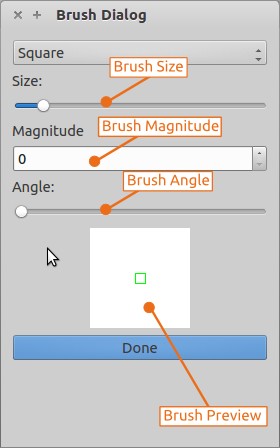
The size slider allows the user to change the width of the brush and each change is immediately reflected in the preview section. Since the brush modifies a Fourier Tranform (which is complex), the brush has a magnitude as well as an angle. The Magnitude spinbox modifies the magnitude of the brush, where as the Angle slider adjusts its angle between 0 and 360. On a click, the brush will update the value of all pixels contained within it to the value specified by its magnitude and angle.

Editing

After selecting a brush, hovering over the frequency domain image generates a green preview of it. In addition to the mouse position (top-left) a secondary preview is shown in the diagonally opposite (bottom-right) quadrant. This is because, the Fourier transform of real images is symmetric about the centre. To maintain the same consistency, the brush also performs symmetric edits. Clicking on the frequency domain image with the brush, applies it and the spatial domain image immediately reflects the change. When a brush is applied, only the magnitude of the fourier transform is affected, the phase remains the same. Since the fourier transform was derived from the Y component of the image, it is the only component affected. This means that only the intensity(Y) of pixels will change, the colour(U and V) will remain the same.

Saving

Only the .png format is supported for saving images. The File > Save Image option will save only the modified spatial domain image.

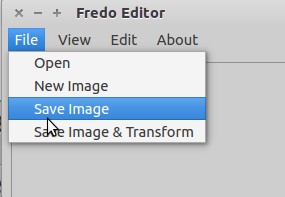
The File > Save Image & Transform option will save the spatial and frequency domain images side-by-side.